VERE - Rev-3 - Plants
Published at Mar 8, 2025
Random number generators can be seeded, making their “random numbers” predictable if you know the seed. That’s what’s going on here. Get the seed, retrieve the numbers, and decrypt the flag.
Not all RNGs are the same - generate the seeded random numbers on a system that can also run this specific binary.
This reverse engineering challenge involves a binary that uses a seeded random number generator (RNG) to encrypt a flag. Our task is to determine the seed, replicate the RNG sequence, and decrypt the flag.
Initial Analysis
We’re given a binary ELF executable. Running the file seems like it is just a flag checker, so we won’t get much info from that.

I opened it up in Ghidra, but saw no main function. Going into the entry function, however, I knew that in the following line, the first argument after __libc_start_main is the main:
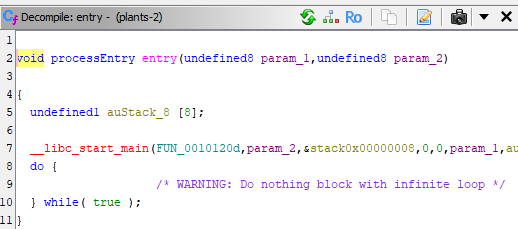
So simply renaming FUN_0010120d to main, I could now identify it in my function tree. Here is the decompiled main function:
undefined8 main(void)
{
char cVar1;
int iVar2;
undefined8 uVar3;
long in_FS_OFFSET;
int local_50;
int local_4c;
char local_48 [40];
long local_20;
local_20 = *(long *)(in_FS_OFFSET + 0x28);
printf("Flag: ");
for (local_50 = 0; local_50 < 0x24; local_50 = local_50 + 1) {
__isoc99_scanf(&DAT_0010200b,local_48 + local_50);
}
local_4c = 0;
do {
if (0x23 < local_4c) {
puts("Correct!!!");
uVar3 = 0;
LAB_00101306:
if (local_20 != *(long *)(in_FS_OFFSET + 0x28)) {
/* WARNING: Subroutine does not return */
__stack_chk_fail();
}
return uVar3;
}
cVar1 = local_48[local_4c];
iVar2 = rand();
if (((int)cVar1 ^ iVar2 % 0x13337) != *(uint *)(&DAT_00104060 + (long)local_4c * 4)) {
puts("Nope");
uVar3 = 1;
goto LAB_00101306;
}
local_4c = local_4c + 1;
} while( true );
}Renaming Variables
I’m not the strongest sight-reader of C code, so I set out determining what each variable does and renaming it to something I could understand. This is the same code as above, but renamed as I understand the variables and types and what they do:
long main(void)
{
int random_value;
long return_code;
long in_FS_OFFSET;
int input_index;
int verify_index;
char input_flag [40];
long canary;
char input_char;
canary = *(long *)(in_FS_OFFSET + 0x28);
printf("Flag: ");
for (input_index = 0; input_index < 0x24; input_index = input_index + 1) {
__isoc99_scanf(&DAT_0010200b,input_flag + input_index);
}
verify_index = 0;
do {
if (0x23 < verify_index) {
puts("Correct!!!");
return_code = 0;
LAB_00101306:
if (canary != *(long *)(in_FS_OFFSET + 0x28)) {
/* WARNING: Subroutine does not return */
__stack_chk_fail();
}
return return_code;
}
input_char = input_flag[verify_index];
random_value = rand();
if (((int)input_char ^ random_value % 0x13337) !=
*(uint *)(&encrypted_flag + (long)verify_index * 4)) {
puts("Nope");
return_code = 1;
goto LAB_00101306;
}
verify_index = verify_index + 1;
} while( true );
}Here are some of the key insights I drew from analyzing the code like this:
The program reads 36 characters (0x24) into input_flag using scanf("%c"). It then loops 36 times, comparing each input character XORed with rand() % 0x13337 against a value in encrypted_flag. This 0x13337 value is the modulo. The encrypted flag is a global array of 36 values (144 bytes), accessed as encrypted_flag[verify_index]. It uses rand(), which is seeded somewhere (but not in main), making the sequence predictable if we find the seed.
The challenge hinges on finding the seed and extracting encrypted_flag. So in order to decrypt the flag, I simply need to find this seed and use it to reverse the XOR like this:
input_char = encrypted_flag[i] ^ (rand() % 0x13337)Locate encrypted_flag
First, we need to find the encrypted values of encrypted_flag. Double-clicking encrypted_flag in the following line:
if (((int)input_char ^ random_value % 0x13337) != *(uint *)(&encrypted_flag + (long)verify_index * 4)) {jumped to its definition at address 0x00104060. The listing view showed 144 bytes, some of which I’ve shown below:
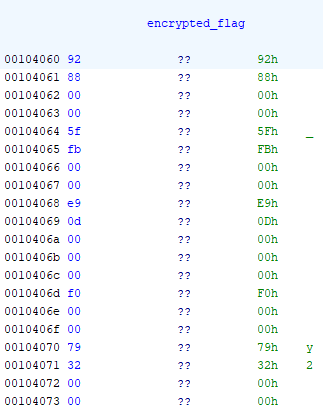
144 bytes is 36 4-byte dwords, which is a familiar number (the size of input_flag) that should get our attention! I organized a few of those bytes into a more comprehendable format to help visualize those dwords:
00104060 92 88 00 00 5f fb 00 00 e9 0d 00 00 00 f0 00 00
00104070 79 32 00 00 72 15 01 00 dc 69 00 00 ca 86 00 00
...
001040e0 0d c2 00 00 7d 54 00 00 c0 27 00 00 09 89 00 00These are big-endian, but that won’t work for what I have in mind. I converted them to little-endian, and threw them into an array of unsigned integers to make an array of the encrypted characters of the flag:
unsigned int encrypted_flag[36] = {
0x00008892, 0x0000fb5f, 0x00000de9, 0x0000f000, 0x00003279, 0x00011572,
0x000069dc, 0x000086ca, 0x000066b6, 0x0000f8ef, 0x0000c710, 0x00005747,
0x00008c8c, 0x000021b4, 0x000064f0, 0x0000d456, 0x00008ff9, 0x000117a1,
0x00009512, 0x00012210, 0x0000c538, 0x0000025f, 0x0000d5f8, 0x00003349,
0x000083ec, 0x00008f65, 0x0000cb96, 0x0000a3d9, 0x00004cfe, 0x0000fa2c,
0x0000468b, 0x0000d515, 0x0000c20d, 0x0000547d, 0x000027c0, 0x00008909
};Taking the R out of RNG
The hint emphasizes a seeded RNG and matching the binary’s environment. Following the Function Call Tree in Ghidra, we can see that main doesn’t call srand(), rather the binary uses glibc’s rand(), which leads me to believe that the seed is set somewhere else. Before I went digging, I did a little research and discovered that a seed value of 1 was the default value, and I hoped that it may have been left as-is.
I wrote a quick script to test this theory, compiled it with gcc -o letitdie letitdie.c (ten points if you get the reference) on a Linux system, and then ran it with ./letitdie. :
#include <stdio.h>
#include <stdlib.h>
int main() {
unsigned int encrypted_flag[36] = {
0x00008892, 0x0000fb5f, 0x00000de9, 0x0000f000, 0x00003279, 0x00011572,
0x000069dc, 0x000086ca, 0x000066b6, 0x0000f8ef, 0x0000c710, 0x00005747,
0x00008c8c, 0x000021b4, 0x000064f0, 0x0000d456, 0x00008ff9, 0x000117a1,
0x00009512, 0x00012210, 0x0000c538, 0x0000025f, 0x0000d5f8, 0x00003349,
0x000083ec, 0x00008f65, 0x0000cb96, 0x0000a3d9, 0x00004cfe, 0x0000fa2c,
0x0000468b, 0x0000d515, 0x0000c20d, 0x0000547d, 0x000027c0, 0x00008909
};
char flag[37] = {0}; // 36 chars + null byte
srand(1); // Default seed
for (int i = 0; i < 36; i++) {
int r = rand() % 0x13337;
flag[i] = (char)(encrypted_flag[i] ^ r);
}
printf("Decrypted flag: %s\n", flag);
return 0;
}This revealed the decrypted flag!

… or not. The output was gibberish. The default seed was not the solution.
To be honest, I didn’t immediately see where the seed was being generated in the decompiled code, so I decided to try to brute force it, since I already had the rest of the pieces.
We know the modulo was 0x13337, and we just figured out the encrypted flag array. I modified the script to try every seed from 1 - 1000, checking for a vere{ that becomes present in the resulting string, which would indicate that I successfully decrypted it.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main() {
unsigned int encrypted_flag[36] = {
0x00008892, 0x0000fb5f, 0x00000de9, 0x0000f000, 0x00003279, 0x00011572,
0x000069dc, 0x000086ca, 0x000066b6, 0x0000f8ef, 0x0000c710, 0x00005747,
0x00008c8c, 0x000021b4, 0x000064f0, 0x0000d456, 0x00008ff9, 0x000117a1,
0x00009512, 0x00012210, 0x0000c538, 0x0000025f, 0x0000d5f8, 0x00003349,
0x000083ec, 0x00008f65, 0x0000cb96, 0x0000a3d9, 0x00004cfe, 0x0000fa2c,
0x0000468b, 0x0000d515, 0x0000c20d, 0x0000547d, 0x000027c0, 0x00008909
};
char flag[37] = {0};
for (int seed = 0; seed < 1000; seed++) {
srand(seed);
printf("Seed: %d\n", seed);
for (int i = 0; i < 36; i++) {
int r = rand() % 0x13337;
flag[i] = (char)(encrypted_flag[i] ^ r);
}
if (strstr(flag, "vere{")) {
printf("Seed: %d\nDecrypted flag: %s\n", seed, flag);
break;
}
}
return 0;
}It ran through my seeds lightning fast, but unfortunately did not find a vere{. I thought for a moment that I’d have to actually keep digging through the decompiled code, but then I realized how fast the brute force worked (nearly instantly for 1000 values), and that I could very reasonably increase that number significantly. I increased the for loop to a million.
for (int seed = 0; seed < 100000; seed++) {It still took less than a half second, and I got a hit!
Seed: 78647
Decrypted flag: vere{faith_is_l1k3_a_little_s33d...}By exploiting the pseudo part of pseudo-randomness and seeding the random function with the value 78647, we can decrypt the flag every time!
Flag: vere{faith_is_l1k3_a_little_s33d...}